Introduction
Data with imbalanced target class occurs frequently in several domians such as credit card Fraud Detection ,insurance claim prediction, email spam detection, anomaly detection, outlier detection etc. Financial instituions loose millions of dollars every year to fraudulent financial transactions. It is important that these institutions are able to identify fraud to protect their customers and also reduce the financial losses that comes from fraudsters.
The goal here is to predict fraudulent transactions to minimize loss to financial companies. For machine learning data with imbalanced target clases, the model evaluation metric is the AUC, the area under the ROC curve and the area under the precision-recall curve. The accuaracy metric is not useful in these situations since usually the proportion of the positive class in these situations is so low that even a naive classifier that predicts all transactions as fraudulent would result in a high accuracy. For example the dataset considered here, the proportion of negative examples is over 99% this a naive classifier can predict all transactions as legitimate and would be over 99% accuarate.
The following packages that is been installed here will be neccessary for some of the analysis later on this project.
!pip uninstall scikit-learn # until no more scikit-learn is present
!pip install scikit-learn
!pip install scikit-optimize
!pip install skll
!pip install imbalanced-learn
!pip install eli5
!pip install scipy
!pip install scikit-optimize
# activate R magic to run R in google colab notebook
import rpy2
%load_ext rpy2.ipython
#%%R
#install.packages("MLmetrics")
#install.packages("yardstick")
#install.packages("mltools")
#install.packages("glue")
%tensorflow_version 2.x
import numpy as np
import pandas as pd
import io
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns; sns.set(style="ticks", color_codes=True)
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler, RobustScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.feature_selection import SelectKBest, f_classif
from sklearn.feature_selection import chi2
from sklearn.linear_model import LogisticRegression
from sklearn import feature_selection
#from sklearn.preprocessing import Imputer
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.metrics import make_scorer
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from sklearn.model_selection import cross_validate
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import RFECV
from xgboost import XGBClassifier
from sklearn.impute import SimpleImputer
import xgboost as xgb
import lightgbm as lgb
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.linear_model import LogisticRegression
from sklearn import svm
from skopt.space import Real, Categorical, Integer
#from skll.metrics import spearman
from scipy.stats import kendalltau, spearmanr, pearsonr
from skopt import BayesSearchCV
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.metrics import make_scorer
from skopt.space import Real, Categorical, Integer
from sklearn.metrics import classification_report
from sklearn.base import TransformerMixin
from sklearn.metrics import classification_report, f1_score, accuracy_score, precision_score, confusion_matrix
from sklearn.metrics import roc_auc_score
from sklearn.metrics import precision_recall_curve
pd.set_option('display.max_rows', 600)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000)
import warnings
import pandas_profiling
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.feature_selection import SelectFromModel
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.pipeline import make_pipeline, FeatureUnion, Pipeline
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.model_selection import GridSearchCV
from imblearn.over_sampling import SMOTE
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.metrics import roc_curve, roc_auc_score,balanced_accuracy_score
from sklearn.svm import SVC
import random
import matplotlib.pyplot as plt
import seaborn as sns
import re
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import ColumnTransformer, make_column_transformer
from imblearn.over_sampling import RandomOverSampler
from imblearn.under_sampling import RandomUnderSampler
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import *
from sklearn.utils import resample
from imblearn.over_sampling import SMOTE
#import smote
import os
from sklearn.tree import DecisionTreeClassifier
from imblearn.metrics import geometric_mean_score as gmean
from imblearn.metrics import make_index_balanced_accuracy as iba
from imblearn.metrics import *
from eli5.sklearn import PermutationImportance
from eli5.sklearn import *
import eli5
from eli5.permutation_importance import get_score_importances
#import rus
# Skopt functions
from skopt import BayesSearchCV
from skopt import gp_minimize # Bayesian optimization using Gaussian Processes
from skopt.space import Real, Categorical, Integer
from skopt.utils import use_named_args # decorator to convert a list of parameters to named arguments
from skopt.callbacks import DeadlineStopper # Stop the optimization before running out of a fixed budget of time.
from skopt.callbacks import VerboseCallback # Callback to control the verbosity
from skopt.callbacks import DeltaXStopper # Stop the optimization If the last two positions at which the objective has been evaluated are less than delta
from joblib import dump, load
from prettytable import PrettyTable
from collections import Counter
from sklearn.datasets import make_classification
from imblearn.under_sampling import RandomUnderSampler # doctest: +NORMALIZE_WHITESPACE
from imblearn import under_sampling, over_sampling
from imblearn.over_sampling import SMOTE
import tensorflow as tf
warnings.filterwarnings("ignore")
%matplotlib inline
#specify tensorflow version to use
%tensorflow_version 2.x
#load tensorboard
#%load_ext tensorboard
#%tensorboard --logdir logs
%autosave 5
Autosaving every 5 seconds
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(missing_values=np.nan, strategy='mean')
Description of Data.
The datasets can be found on kaggle.The link to it is here.
The datasets contains transactions made by credit cards in September 2013 by european cardholders. This dataset presents transactions that occurred in two days, where we have 492 frauds out of 284,807 transactions. The dataset is highly imbalanced, the positive class (frauds) account for 0.172% of all transactions.
It contains only numerical input variables which are the result of a PCA transformation. This was done to preserve the identity and privacy of the people whose transaction this data was gathered from. Features V1, V2, … V28 are the principal components obtained with PCA, the only features which have not been transformed with PCA are ‘Time’ and ‘Amount’. Feature ‘Time’ contains the seconds elapsed between each transaction and the first transaction in the dataset. The feature ‘Amount’ is the transaction Amount, this feature can be used for example-dependant cost-senstive learning. Feature ‘Class’ is the response variable and it takes value 1 in case of fraud and 0 otherwise.
file = tf.keras.utils
df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
df.head()
|
Time |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
V10 |
V11 |
V12 |
V13 |
V14 |
V15 |
V16 |
V17 |
V18 |
V19 |
V20 |
V21 |
V22 |
V23 |
V24 |
V25 |
V26 |
V27 |
V28 |
Amount |
Class |
| 0 |
0.0 |
-1.359807 |
-0.072781 |
2.536347 |
1.378155 |
-0.338321 |
0.462388 |
0.239599 |
0.098698 |
0.363787 |
0.090794 |
-0.551600 |
-0.617801 |
-0.991390 |
-0.311169 |
1.468177 |
-0.470401 |
0.207971 |
0.025791 |
0.403993 |
0.251412 |
-0.018307 |
0.277838 |
-0.110474 |
0.066928 |
0.128539 |
-0.189115 |
0.133558 |
-0.021053 |
149.62 |
0 |
| 1 |
0.0 |
1.191857 |
0.266151 |
0.166480 |
0.448154 |
0.060018 |
-0.082361 |
-0.078803 |
0.085102 |
-0.255425 |
-0.166974 |
1.612727 |
1.065235 |
0.489095 |
-0.143772 |
0.635558 |
0.463917 |
-0.114805 |
-0.183361 |
-0.145783 |
-0.069083 |
-0.225775 |
-0.638672 |
0.101288 |
-0.339846 |
0.167170 |
0.125895 |
-0.008983 |
0.014724 |
2.69 |
0 |
| 2 |
1.0 |
-1.358354 |
-1.340163 |
1.773209 |
0.379780 |
-0.503198 |
1.800499 |
0.791461 |
0.247676 |
-1.514654 |
0.207643 |
0.624501 |
0.066084 |
0.717293 |
-0.165946 |
2.345865 |
-2.890083 |
1.109969 |
-0.121359 |
-2.261857 |
0.524980 |
0.247998 |
0.771679 |
0.909412 |
-0.689281 |
-0.327642 |
-0.139097 |
-0.055353 |
-0.059752 |
378.66 |
0 |
| 3 |
1.0 |
-0.966272 |
-0.185226 |
1.792993 |
-0.863291 |
-0.010309 |
1.247203 |
0.237609 |
0.377436 |
-1.387024 |
-0.054952 |
-0.226487 |
0.178228 |
0.507757 |
-0.287924 |
-0.631418 |
-1.059647 |
-0.684093 |
1.965775 |
-1.232622 |
-0.208038 |
-0.108300 |
0.005274 |
-0.190321 |
-1.175575 |
0.647376 |
-0.221929 |
0.062723 |
0.061458 |
123.50 |
0 |
| 4 |
2.0 |
-1.158233 |
0.877737 |
1.548718 |
0.403034 |
-0.407193 |
0.095921 |
0.592941 |
-0.270533 |
0.817739 |
0.753074 |
-0.822843 |
0.538196 |
1.345852 |
-1.119670 |
0.175121 |
-0.451449 |
-0.237033 |
-0.038195 |
0.803487 |
0.408542 |
-0.009431 |
0.798278 |
-0.137458 |
0.141267 |
-0.206010 |
0.502292 |
0.219422 |
0.215153 |
69.99 |
0 |
df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe().transpose()
|
count |
mean |
std |
min |
25% |
50% |
75% |
max |
| Time |
284807.0 |
9.481386e+04 |
47488.145955 |
0.000000 |
54201.500000 |
84692.000000 |
139320.500000 |
172792.000000 |
| V1 |
284807.0 |
3.919560e-15 |
1.958696 |
-56.407510 |
-0.920373 |
0.018109 |
1.315642 |
2.454930 |
| V2 |
284807.0 |
5.688174e-16 |
1.651309 |
-72.715728 |
-0.598550 |
0.065486 |
0.803724 |
22.057729 |
| V3 |
284807.0 |
-8.769071e-15 |
1.516255 |
-48.325589 |
-0.890365 |
0.179846 |
1.027196 |
9.382558 |
| V4 |
284807.0 |
2.782312e-15 |
1.415869 |
-5.683171 |
-0.848640 |
-0.019847 |
0.743341 |
16.875344 |
| V5 |
284807.0 |
-1.552563e-15 |
1.380247 |
-113.743307 |
-0.691597 |
-0.054336 |
0.611926 |
34.801666 |
| V26 |
284807.0 |
1.699104e-15 |
0.482227 |
-2.604551 |
-0.326984 |
-0.052139 |
0.240952 |
3.517346 |
| V27 |
284807.0 |
-3.660161e-16 |
0.403632 |
-22.565679 |
-0.070840 |
0.001342 |
0.091045 |
31.612198 |
| V28 |
284807.0 |
-1.206049e-16 |
0.330083 |
-15.430084 |
-0.052960 |
0.011244 |
0.078280 |
33.847808 |
| Amount |
284807.0 |
8.834962e+01 |
250.120109 |
0.000000 |
5.600000 |
22.000000 |
77.165000 |
25691.160000 |
| Class |
284807.0 |
1.727486e-03 |
0.041527 |
0.000000 |
0.000000 |
0.000000 |
0.000000 |
1.000000 |
We can see the target class is highly imbalanced. The minority classis about 0.17% of the target exampes.
df['Class'].value_counts(normalize=True)*100
0 99.827251
1 0.172749
Name: Class, dtype: float64
neg, pos = df.Class.value_counts()
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n '.format(
total, pos, 100 * pos / total,100 * neg / total))
print('Total: {}\n Negative: {} ({:.2f}% of total)\n '.format(
total, neg, 100 * neg / total))
Examples:
Total: 284807
Positive: 492 (0.17% of total)
Total: 284807
Negative: 284315 (99.83% of total)
#x = raw_df.drop(['Time'],axis=1)
# Use a utility from sklearn to split and shuffle our dataset.
train_df, test_df = train_test_split(df, test_size=0.2)
#train_df, val_df = train_test_split(train_df, test_size=0.2)
train_x =train_df.drop(['Time','Class'],axis=1)
test_x = test_df.drop(['Time','Class'],axis=1)
#val_x = val_df.drop(['Time'],axis=1)
train_y= train_df.Class
test_y = test_df.Class
#val_y = val_df.Class
print('Traing dataset size:{}'.format(train_x.shape))
print('Test dataset size:{}'.format(test_x.shape))
#print('Validation dataset size: {}'.format(val_df.shape))
Traing dataset size:(227845, 29)
Test dataset size:(56962, 29)
#train_x.columns
#test_x.columns
test_y.isna().sum()
The first model considered here is the extreme gradient boosting algorithm. It is popular with modeling tabular data. The hyperparameters of the model would be set to default except the scale_pos_weight which would be tuned in the case of cost-sensitive xgboost to find the best weight that optimizes the model.The hyperparameter values is left to the default values to allow for a fair comparison among machine learning algorithms used in this analysis. The hyperparameter tuning is done by bayesian optimization using the scikit-optimize package.
# Setting a 5-fold stratified cross-validation (note: shuffle=True)
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)
clf = xgb.XGBClassifier(
n_jobs = -1,
objective = 'binary:logistic',
silent=1,
tree_method='approx')
search_spaces = {
#'learning_rate': Real(0.01, 1.0, 'log-uniform'),
# 'min_child_weight': Integer(0, 10),
# 'max_depth': Integer(1, 50),
# 'max_delta_step': Integer(0, 20), # Maximum delta step we allow each leaf output
# 'subsample': Real(0.01, 1.0, 'uniform'),
# 'colsample_bytree': Real(0.01, 1.0, 'uniform'), # subsample ratio of columns by tree
# 'colsample_bylevel': Real(0.01, 1.0, 'uniform'), # subsample ratio by level in trees
#'reg_lambda': Real(1e-9, 1000, 'log-uniform'), # L2 regularization
#'reg_alpha': Real(1e-9, 1.0, 'log-uniform'), # L1 regularization
# 'gamma': Real(1e-9, 0.5, 'log-uniform'), # Minimum loss reduction for partition/pruning parameter
# 'n_estimators': Integer(50, 100),
'scale_pos_weight': Real(1e-6, 2000, 'log-uniform')
}
bayessearch = BayesSearchCV(clf,
search_spaces,
scoring='roc_auc', #f1
cv=skf,
n_iter=40,
n_jobs=-1,
return_train_score=False,
#refit=True,
optimizer_kwargs={'base_estimator': 'GP'},
random_state=22)
#xgbm_model = bayessearch.fit(X=train_x, y=train_y)
from google.colab import drive
drive.mount('/content/drive')
Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).
#share_link="https://drive.google.com/file/d/1mGzO4-vaTKVgH5zzzXCVcXNbj-Bt8u8g/view?usp=sharing"
import os
os.getcwd()
#!files.os.listdir()
Build Pandas -Profiling Report
The exploratory analysis of the features in the dataset can be automated with the Pandas -ProfilingReport package. It generates exploratory plots of the features in a dataset that is passed to it.
#Inline report without saving object
pandas_profiling.ProfileReport(df)
#Save report to file¶
pfr = pandas_profiling.ProfileReport(df)
pfr.to_file("/content/drive/My Drive/profilingReport2.html")
pfr
Dataset info
| Number of variables |
31 |
| Number of observations |
284807 |
| Total Missing (%) |
0.0% |
| Total size in memory |
67.4 MiB |
| Average record size in memory |
248.0 B |
Variables types
| Numeric |
30 |
| Categorical |
0 |
| Boolean |
1 |
| Date |
0 |
| Text (Unique) |
0 |
| Rejected |
0 |
| Unsupported |
0 |
Warnings
- Dataset has 1081 duplicate rows Warning
| Distinct count |
124592 |
| Unique (%) |
43.7% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
94814 |
| Minimum |
0 |
| Maximum |
172790 |
| Zeros (%) |
0.0% |
Quantile statistics
| Minimum |
0 |
| 5-th percentile |
25298 |
| Q1 |
54202 |
| Median |
84692 |
| Q3 |
139320 |
| 95-th percentile |
164140 |
| Maximum |
172790 |
| Range |
172790 |
| Interquartile range |
85119 |
Descriptive statistics
| Standard deviation |
47488 |
| Coef of variation |
0.50086 |
| Kurtosis |
-1.2935 |
| Mean |
94814 |
| MAD |
42796 |
| Skewness |
-0.035568 |
| Sum |
27004000000 |
| Variance |
2255100000 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 163152.0 |
36 |
0.0% |
|
| 64947.0 |
26 |
0.0% |
|
| 68780.0 |
25 |
0.0% |
|
| 3767.0 |
21 |
0.0% |
|
| 3770.0 |
20 |
0.0% |
|
| 128860.0 |
19 |
0.0% |
|
| 19912.0 |
19 |
0.0% |
|
| 3750.0 |
19 |
0.0% |
|
| 140347.0 |
19 |
0.0% |
|
| 143083.0 |
18 |
0.0% |
|
| Other values (124582) |
284585 |
99.9% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| 0.0 |
2 |
0.0% |
|
| 1.0 |
2 |
0.0% |
|
| 2.0 |
2 |
0.0% |
|
| 4.0 |
1 |
0.0% |
|
| 7.0 |
2 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 172785.0 |
1 |
0.0% |
|
| 172786.0 |
1 |
0.0% |
|
| 172787.0 |
1 |
0.0% |
|
| 172788.0 |
2 |
0.0% |
|
| 172792.0 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
3.9196e-15 |
| Minimum |
-56.408 |
| Maximum |
2.4549 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-56.408 |
| 5-th percentile |
-2.8991 |
| Q1 |
-0.92037 |
| Median |
0.018109 |
| Q3 |
1.3156 |
| 95-th percentile |
2.0812 |
| Maximum |
2.4549 |
| Range |
58.862 |
| Interquartile range |
2.236 |
Descriptive statistics
| Standard deviation |
1.9587 |
| Coef of variation |
499720000000000 |
| Kurtosis |
32.487 |
| Mean |
3.9196e-15 |
| MAD |
1.4116 |
| Skewness |
-3.2807 |
| Sum |
3.3208e-1 |
| Variance |
3.8365 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 2.0557970063003896 |
77 |
0.0% |
|
| 1.24567381944824 |
77 |
0.0% |
|
| 2.0533112135278504 |
62 |
0.0% |
|
| 1.30237796508637 |
60 |
0.0% |
|
| 2.04021105776632 |
53 |
0.0% |
|
| 2.08517487552541 |
48 |
0.0% |
|
| 1.33284931179458 |
45 |
0.0% |
|
| 1.01841181981555 |
40 |
0.0% |
|
| 1.33505315377059 |
39 |
0.0% |
|
| 1.3154041716379299 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -56.407509631329 |
1 |
0.0% |
|
| -46.85504720078179 |
1 |
0.0% |
|
| -41.9287375244141 |
1 |
0.0% |
|
| -40.4701418378475 |
1 |
0.0% |
|
| -40.0425374953845 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 2.4305067805687406 |
1 |
0.0% |
|
| 2.43920748106102 |
1 |
0.0% |
|
| 2.44650498499596 |
1 |
0.0% |
|
| 2.4518884899535895 |
1 |
0.0% |
|
| 2.45492999121121 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
5.6882e-16 |
| Minimum |
-72.716 |
| Maximum |
22.058 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-72.716 |
| 5-th percentile |
-1.972 |
| Q1 |
-0.59855 |
| Median |
0.065486 |
| Q3 |
0.80372 |
| 95-th percentile |
1.8086 |
| Maximum |
22.058 |
| Range |
94.773 |
| Interquartile range |
1.4023 |
Descriptive statistics
| Standard deviation |
1.6513 |
| Coef of variation |
2903100000000000 |
| Kurtosis |
95.773 |
| Mean |
5.6882e-16 |
| MAD |
0.97384 |
| Skewness |
-4.6249 |
| Sum |
9.7316e-11 |
| Variance |
2.7268 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.166975019545401 |
77 |
0.0% |
|
| -0.32666777306077005 |
77 |
0.0% |
|
| 0.08973464781763099 |
62 |
0.0% |
|
| -0.606529308236609 |
60 |
0.0% |
|
| -0.146974974784838 |
53 |
0.0% |
|
| 0.39305057772255 |
48 |
0.0% |
|
| 0.38919824918427603 |
45 |
0.0% |
|
| 1.03666300867632 |
40 |
0.0% |
|
| 0.331464026372479 |
39 |
0.0% |
|
| 0.44747360617094895 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -72.7157275629303 |
1 |
0.0% |
|
| -63.3446983175027 |
1 |
0.0% |
|
| -60.4646176556493 |
1 |
0.0% |
|
| -50.3832691251379 |
1 |
0.0% |
|
| -48.060856024869395 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 18.1836264596211 |
1 |
0.0% |
|
| 18.902452840124898 |
1 |
0.0% |
|
| 19.167239010306197 |
1 |
0.0% |
|
| 21.4672029942752 |
1 |
0.0% |
|
| 22.0577289904909 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-8.7691e-15 |
| Minimum |
-48.326 |
| Maximum |
9.3826 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-48.326 |
| 5-th percentile |
-2.3897 |
| Q1 |
-0.89036 |
| Median |
0.17985 |
| Q3 |
1.0272 |
| 95-th percentile |
2.0626 |
| Maximum |
9.3826 |
| Range |
57.708 |
| Interquartile range |
1.9176 |
Descriptive statistics
| Standard deviation |
1.5163 |
| Coef of variation |
-172910000000000 |
| Kurtosis |
26.62 |
| Mean |
-8.7691e-15 |
| MAD |
1.1337 |
| Skewness |
-2.2402 |
| Sum |
-3.9108e-1 |
| Variance |
2.299 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -2.75204095570008 |
77 |
0.0% |
|
| 0.488305742562781 |
77 |
0.0% |
|
| -1.68183566862495 |
62 |
0.0% |
|
| -0.681986192919261 |
60 |
0.0% |
|
| -2.95593366483195 |
53 |
0.0% |
|
| -4.50820053235418 |
48 |
0.0% |
|
| -2.16559660467804 |
45 |
0.0% |
|
| -1.6898137072248403 |
40 |
0.0% |
|
| -2.05776277666682 |
39 |
0.0% |
|
| -0.495757487926775 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -48.3255893623954 |
1 |
0.0% |
|
| -33.6809840183525 |
1 |
0.0% |
|
| -32.9653457595238 |
1 |
0.0% |
|
| -32.45419818625469 |
1 |
0.0% |
|
| -31.8135859546007 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 4.07916781154883 |
1 |
0.0% |
|
| 4.10171617761651 |
1 |
0.0% |
|
| 4.18781059904763 |
1 |
0.0% |
|
| 4.22610848028397 |
1 |
0.0% |
|
| 9.38255843282114 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
2.7823e-15 |
| Minimum |
-5.6832 |
| Maximum |
16.875 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-5.6832 |
| 5-th percentile |
-2.1957 |
| Q1 |
-0.84864 |
| Median |
-0.019847 |
| Q3 |
0.74334 |
| 95-th percentile |
2.5665 |
| Maximum |
16.875 |
| Range |
22.559 |
| Interquartile range |
1.592 |
Descriptive statistics
| Standard deviation |
1.4159 |
| Coef of variation |
508880000000000 |
| Kurtosis |
2.6355 |
| Mean |
2.7823e-15 |
| MAD |
1.0603 |
| Skewness |
0.67629 |
| Sum |
5.9435e-1 |
| Variance |
2.0047 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.842316033286871 |
77 |
0.0% |
|
| 0.6353219207244001 |
77 |
0.0% |
|
| 0.45421196023303295 |
62 |
0.0% |
|
| -1.9046033962221203 |
60 |
0.0% |
|
| -0.5783559788671391 |
53 |
0.0% |
|
| -0.311770683288625 |
48 |
0.0% |
|
| -0.306872623831362 |
45 |
0.0% |
|
| 1.31547583332268 |
40 |
0.0% |
|
| -0.346175355279224 |
39 |
0.0% |
|
| -0.557087388354872 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -5.68317119816995 |
1 |
0.0% |
|
| -5.600607141215099 |
1 |
0.0% |
|
| -5.56011758115594 |
1 |
0.0% |
|
| -5.519697123284151 |
1 |
0.0% |
|
| -5.416315392339291 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 13.1436680982574 |
1 |
0.0% |
|
| 15.3041839851875 |
1 |
0.0% |
|
| 16.4912171736623 |
1 |
0.0% |
|
| 16.7155373723131 |
1 |
0.0% |
|
| 16.8753440335975 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-1.5526e-15 |
| Minimum |
-113.74 |
| Maximum |
34.802 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-113.74 |
| 5-th percentile |
-1.702 |
| Q1 |
-0.6916 |
| Median |
-0.054336 |
| Q3 |
0.61193 |
| 95-th percentile |
2.099 |
| Maximum |
34.802 |
| Range |
148.54 |
| Interquartile range |
1.3035 |
Descriptive statistics
| Standard deviation |
1.3802 |
| Coef of variation |
-889010000000000 |
| Kurtosis |
206.9 |
| Mean |
-1.5526e-15 |
| MAD |
0.89707 |
| Skewness |
-2.4259 |
| Sum |
2.7353e-1 |
| Variance |
1.9051 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 2.46307225982454 |
77 |
0.0% |
|
| -0.5627766807738629 |
77 |
0.0% |
|
| 0.298310371498215 |
62 |
0.0% |
|
| 1.3266231068468501 |
60 |
0.0% |
|
| 2.60935827084169 |
53 |
0.0% |
|
| 3.51011694221752 |
48 |
0.0% |
|
| 2.6413512514436 |
45 |
0.0% |
|
| 1.69843605562986 |
40 |
0.0% |
|
| 2.58323382235421 |
39 |
0.0% |
|
| 2.70504105264306 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -113.74330671114599 |
1 |
0.0% |
|
| -42.1478983728015 |
1 |
0.0% |
|
| -40.4277263001722 |
1 |
0.0% |
|
| -35.1821203113785 |
1 |
0.0% |
|
| -32.0921290046357 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 29.1621720203733 |
1 |
0.0% |
|
| 31.457046054914304 |
1 |
0.0% |
|
| 32.9114617007293 |
1 |
0.0% |
|
| 34.0993093435765 |
1 |
0.0% |
|
| 34.8016658766686 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
2.0107e-15 |
| Minimum |
-26.161 |
| Maximum |
73.302 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-26.161 |
| 5-th percentile |
-1.4068 |
| Q1 |
-0.7683 |
| Median |
-0.27419 |
| Q3 |
0.39856 |
| 95-th percentile |
3.1604 |
| Maximum |
73.302 |
| Range |
99.462 |
| Interquartile range |
1.1669 |
Descriptive statistics
| Standard deviation |
1.3323 |
| Coef of variation |
662600000000000 |
| Kurtosis |
42.642 |
| Mean |
2.0107e-15 |
| MAD |
0.90901 |
| Skewness |
1.8266 |
| Sum |
4.2439e-1 |
| Variance |
1.7749 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -1.01107261632698 |
77 |
0.0% |
|
| 3.17385642307029 |
77 |
0.0% |
|
| -0.953526086363083 |
62 |
0.0% |
|
| 3.43631244725031 |
60 |
0.0% |
|
| 3.1426415310887905 |
53 |
0.0% |
|
| 2.45329922016311 |
48 |
0.0% |
|
| 2.80808376427436 |
45 |
0.0% |
|
| 0.528806548957574 |
40 |
0.0% |
|
| 2.8541019971666097 |
39 |
0.0% |
|
| 2.7624395847487797 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -26.1605059358433 |
1 |
0.0% |
|
| -23.496713929871397 |
1 |
0.0% |
|
| -21.9293122885031 |
1 |
0.0% |
|
| -21.2487516200394 |
1 |
0.0% |
|
| -20.8696261884133 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 21.3930687572539 |
1 |
0.0% |
|
| 21.550496192579605 |
1 |
0.0% |
|
| 22.5292984665587 |
1 |
0.0% |
|
| 23.9178371266367 |
1 |
0.0% |
|
| 73.3016255459646 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-1.6942e-15 |
| Minimum |
-43.557 |
| Maximum |
120.59 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-43.557 |
| 5-th percentile |
-1.4344 |
| Q1 |
-0.55408 |
| Median |
0.040103 |
| Q3 |
0.57044 |
| 95-th percentile |
1.4076 |
| Maximum |
120.59 |
| Range |
164.15 |
| Interquartile range |
1.1245 |
Descriptive statistics
| Standard deviation |
1.2371 |
| Coef of variation |
-730170000000000 |
| Kurtosis |
405.61 |
| Mean |
-1.6942e-15 |
| MAD |
0.73785 |
| Skewness |
2.5539 |
| Sum |
-1.5825e-1 |
| Variance |
1.5304 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.43212592398782396 |
77 |
0.0% |
|
| 0.0149526614685896 |
77 |
0.0% |
|
| 0.152002545314135 |
62 |
0.0% |
|
| -1.14512682747431 |
60 |
0.0% |
|
| -0.41688284124123 |
53 |
0.0% |
|
| 0.220468581007954 |
48 |
0.0% |
|
| -0.171626636099457 |
45 |
0.0% |
|
| 0.33171450239883 |
40 |
0.0% |
|
| -0.18754733727697498 |
39 |
0.0% |
|
| -0.5349938273164451 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -43.5572415712451 |
1 |
0.0% |
|
| -41.5067960832574 |
1 |
0.0% |
|
| -37.0603114554112 |
1 |
0.0% |
|
| -33.2393281671892 |
1 |
0.0% |
|
| -31.76494649021 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 34.3031768568354 |
1 |
0.0% |
|
| 36.6772679454031 |
1 |
0.0% |
|
| 36.877368268259794 |
1 |
0.0% |
|
| 44.054461363163796 |
1 |
0.0% |
|
| 120.589493945238 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-1.927e-16 |
| Minimum |
-73.217 |
| Maximum |
20.007 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-73.217 |
| 5-th percentile |
-0.84215 |
| Q1 |
-0.20863 |
| Median |
0.022358 |
| Q3 |
0.32735 |
| 95-th percentile |
1.05 |
| Maximum |
20.007 |
| Range |
93.224 |
| Interquartile range |
0.53598 |
Descriptive statistics
| Standard deviation |
1.1944 |
| Coef of variation |
-6197900000000000 |
| Kurtosis |
220.59 |
| Mean |
-1.927e-16 |
| MAD |
0.50574 |
| Skewness |
-8.5219 |
| Sum |
3.3538e-11 |
| Variance |
1.4265 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.16021086330181197 |
77 |
0.0% |
|
| 0.7277062007278241 |
77 |
0.0% |
|
| -0.207071379659966 |
62 |
0.0% |
|
| 0.9591472620923409 |
60 |
0.0% |
|
| 0.7843929483197328 |
53 |
0.0% |
|
| 0.543376800596399 |
48 |
0.0% |
|
| 0.683351733616692 |
45 |
0.0% |
|
| 0.364538761567697 |
40 |
0.0% |
|
| 0.6851537704418591 |
39 |
0.0% |
|
| 0.8082500983641501 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -73.21671845526741 |
1 |
0.0% |
|
| -50.94336886770229 |
1 |
0.0% |
|
| -50.688419356750295 |
1 |
0.0% |
|
| -50.420090064434206 |
1 |
0.0% |
|
| -41.484822506637705 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 18.709254543323397 |
1 |
0.0% |
|
| 18.7488719520883 |
1 |
0.0% |
|
| 19.168327389730102 |
1 |
0.0% |
|
| 19.5877726234404 |
1 |
0.0% |
|
| 20.0072083651213 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-3.137e-15 |
| Minimum |
-13.434 |
| Maximum |
15.595 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-13.434 |
| 5-th percentile |
-1.7584 |
| Q1 |
-0.6431 |
| Median |
-0.051429 |
| Q3 |
0.59714 |
| 95-th percentile |
1.7808 |
| Maximum |
15.595 |
| Range |
29.029 |
| Interquartile range |
1.2402 |
Descriptive statistics
| Standard deviation |
1.0986 |
| Coef of variation |
-350210000000000 |
| Kurtosis |
3.7313 |
| Mean |
-3.137e-15 |
| MAD |
0.81439 |
| Skewness |
0.55468 |
| Sum |
-6.8538e-1 |
| Variance |
1.207 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.17036185217373 |
77 |
0.0% |
|
| 0.608605870267216 |
77 |
0.0% |
|
| 0.587335266422761 |
62 |
0.0% |
|
| 1.67130156362918 |
60 |
0.0% |
|
| 0.359902378888007 |
53 |
0.0% |
|
| -0.10043390489717 |
48 |
0.0% |
|
| -0.29796200128389 |
45 |
0.0% |
|
| -0.7117979387642629 |
40 |
0.0% |
|
| -0.28661406862562394 |
39 |
0.0% |
|
| 0.6977195955056469 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -13.4340663182301 |
1 |
0.0% |
|
| -13.3201546920984 |
1 |
0.0% |
|
| -11.1266235224579 |
1 |
0.0% |
|
| -10.8425258685569 |
1 |
0.0% |
|
| -9.48145633401495 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 10.3261330490616 |
1 |
0.0% |
|
| 10.348406697766801 |
1 |
0.0% |
|
| 10.370657984046 |
1 |
0.0% |
|
| 10.392888824678499 |
1 |
0.0% |
|
| 15.5949946071278 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
1.7686e-15 |
| Minimum |
-24.588 |
| Maximum |
23.745 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-24.588 |
| 5-th percentile |
-1.3386 |
| Q1 |
-0.53543 |
| Median |
-0.092917 |
| Q3 |
0.45392 |
| 95-th percentile |
1.5486 |
| Maximum |
23.745 |
| Range |
48.333 |
| Interquartile range |
0.98935 |
Descriptive statistics
| Standard deviation |
1.0888 |
| Coef of variation |
615650000000000 |
| Kurtosis |
31.988 |
| Mean |
1.7686e-15 |
| MAD |
0.69512 |
| Skewness |
1.1871 |
| Sum |
6.379e-1 |
| Variance |
1.1856 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.0445745893804268 |
77 |
0.0% |
|
| -0.0751861699398929 |
77 |
0.0% |
|
| -0.362047348389396 |
62 |
0.0% |
|
| -1.02294602983554 |
60 |
0.0% |
|
| -0.351075101407957 |
53 |
0.0% |
|
| -1.01862219976658 |
48 |
0.0% |
|
| -0.652096600406493 |
45 |
0.0% |
|
| -1.57028828006989 |
40 |
0.0% |
|
| -0.5359027354525039 |
39 |
0.0% |
|
| -1.09018090617913 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -24.5882624372475 |
1 |
0.0% |
|
| -24.403184969972802 |
1 |
0.0% |
|
| -23.2282548357516 |
1 |
0.0% |
|
| -22.1870885620007 |
4 |
0.0% |
|
| -20.949191554361104 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 13.8117577662908 |
1 |
0.0% |
|
| 15.236028204007098 |
1 |
0.0% |
|
| 15.2456856915255 |
1 |
0.0% |
|
| 15.3317415557881 |
1 |
0.0% |
|
| 23.7451361206545 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
9.1703e-16 |
| Minimum |
-4.7975 |
| Maximum |
12.019 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-4.7975 |
| 5-th percentile |
-1.5719 |
| Q1 |
-0.76249 |
| Median |
-0.032757 |
| Q3 |
0.73959 |
| 95-th percentile |
1.614 |
| Maximum |
12.019 |
| Range |
16.816 |
| Interquartile range |
1.5021 |
Descriptive statistics
| Standard deviation |
1.0207 |
| Coef of variation |
1113100000000000 |
| Kurtosis |
1.6339 |
| Mean |
9.1703e-16 |
| MAD |
0.83126 |
| Skewness |
0.35651 |
| Sum |
4.7658e-1 |
| Variance |
1.0419 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.35674901847752005 |
77 |
0.0% |
|
| 0.0635044576008839 |
77 |
0.0% |
|
| -0.589598040395407 |
62 |
0.0% |
|
| -0.19142297265161498 |
60 |
0.0% |
|
| 0.329650883701029 |
53 |
0.0% |
|
| 0.8070381066842709 |
48 |
0.0% |
|
| 0.418002664896219 |
45 |
0.0% |
|
| 3.46301782070354 |
40 |
0.0% |
|
| 0.332848417624034 |
39 |
0.0% |
|
| -0.0286089299546822 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -4.79747346479757 |
1 |
0.0% |
|
| -4.682930547652759 |
1 |
0.0% |
|
| -4.568390246460219 |
1 |
0.0% |
|
| -4.45385284150054 |
1 |
0.0% |
|
| -4.3393186545773705 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 11.228470279576001 |
1 |
0.0% |
|
| 11.277920727806698 |
1 |
0.0% |
|
| 11.6197234753825 |
1 |
0.0% |
|
| 11.6692047358121 |
1 |
0.0% |
|
| 12.018913181619899 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-1.8107e-15 |
| Minimum |
-18.684 |
| Maximum |
7.8484 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-18.684 |
| 5-th percentile |
-1.9672 |
| Q1 |
-0.40557 |
| Median |
0.14003 |
| Q3 |
0.61824 |
| 95-th percentile |
1.2431 |
| Maximum |
7.8484 |
| Range |
26.532 |
| Interquartile range |
1.0238 |
Descriptive statistics
| Standard deviation |
0.9992 |
| Coef of variation |
-551840000000000 |
| Kurtosis |
20.242 |
| Mean |
-1.8107e-15 |
| MAD |
0.70536 |
| Skewness |
-2.2784 |
| Sum |
-3.5743e-1 |
| Variance |
0.9984 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.350563573253678 |
77 |
0.0% |
|
| -0.0734595173503765 |
77 |
0.0% |
|
| -0.17471205308176502 |
62 |
0.0% |
|
| 0.6310273414871078 |
60 |
0.0% |
|
| 0.18350812062465602 |
53 |
0.0% |
|
| -0.330547627789277 |
48 |
0.0% |
|
| -0.32243692372967503 |
45 |
0.0% |
|
| 0.5384113631159171 |
40 |
0.0% |
|
| -0.26831873850147697 |
39 |
0.0% |
|
| 0.0736565150203547 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -18.683714633344298 |
1 |
0.0% |
|
| -18.553697009645802 |
1 |
0.0% |
|
| -18.4311310279993 |
1 |
0.0% |
|
| -18.047596570821604 |
1 |
0.0% |
|
| -17.7691434633638 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 4.4063382205176 |
1 |
0.0% |
|
| 4.4729205841361 |
1 |
0.0% |
|
| 4.57408224145334 |
1 |
0.0% |
|
| 4.84645240859009 |
1 |
0.0% |
|
| 7.8483920756445995 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
1.6934e-15 |
| Minimum |
-5.7919 |
| Maximum |
7.1269 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-5.7919 |
| 5-th percentile |
-1.6397 |
| Q1 |
-0.64854 |
| Median |
-0.013568 |
| Q3 |
0.6625 |
| 95-th percentile |
1.6079 |
| Maximum |
7.1269 |
| Range |
12.919 |
| Interquartile range |
1.311 |
Descriptive statistics
| Standard deviation |
0.99527 |
| Coef of variation |
587720000000000 |
| Kurtosis |
0.1953 |
| Mean |
1.6934e-15 |
| MAD |
0.7846 |
| Skewness |
0.065233 |
| Sum |
2.3286e-1 |
| Variance |
0.99057 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.141238322200309 |
77 |
0.0% |
|
| -0.517759694198053 |
77 |
0.0% |
|
| -0.6211270614210049 |
62 |
0.0% |
|
| 0.0319072703534055 |
60 |
0.0% |
|
| -0.27291854500254503 |
53 |
0.0% |
|
| -0.5314186516713479 |
48 |
0.0% |
|
| -0.143469154599387 |
45 |
0.0% |
|
| -0.37809538452842295 |
40 |
0.0% |
|
| -0.12761419581231198 |
39 |
0.0% |
|
| -0.23845703149556197 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -5.7918812063208405 |
1 |
0.0% |
|
| -4.00863979207158 |
1 |
0.0% |
|
| -3.9617575357502504 |
1 |
0.0% |
|
| -3.8886062856691 |
1 |
0.0% |
|
| -3.8811062494802897 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 4.36999837897829 |
1 |
0.0% |
|
| 4.465413177090861 |
1 |
0.0% |
|
| 4.46956619153499 |
1 |
0.0% |
|
| 4.56900895856606 |
1 |
0.0% |
|
| 7.126882958593759 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
1.479e-15 |
| Minimum |
-19.214 |
| Maximum |
10.527 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-19.214 |
| 5-th percentile |
-1.4394 |
| Q1 |
-0.42557 |
| Median |
0.050601 |
| Q3 |
0.49315 |
| 95-th percentile |
1.3937 |
| Maximum |
10.527 |
| Range |
29.741 |
| Interquartile range |
0.91872 |
Descriptive statistics
| Standard deviation |
0.9586 |
| Coef of variation |
648120000000000 |
| Kurtosis |
23.879 |
| Mean |
1.479e-15 |
| MAD |
0.64865 |
| Skewness |
-1.9952 |
| Sum |
3.4356e-1 |
| Variance |
0.91891 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.40696893438373105 |
77 |
0.0% |
|
| 0.690971618395625 |
77 |
0.0% |
|
| -0.7035127839833039 |
62 |
0.0% |
|
| -0.0314253812628428 |
60 |
0.0% |
|
| -0.597436665174528 |
53 |
0.0% |
|
| -2.1814488246367403 |
48 |
0.0% |
|
| -1.1545242958661899 |
45 |
0.0% |
|
| -3.0454951796322502 |
40 |
0.0% |
|
| -0.868299960850499 |
39 |
0.0% |
|
| 0.215738138536011 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -19.2143254902614 |
1 |
0.0% |
|
| -18.8220867423816 |
1 |
0.0% |
|
| -18.4937733551053 |
1 |
0.0% |
|
| -18.392091495673 |
1 |
0.0% |
|
| -18.049997689859396 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 7.518402781245941 |
1 |
0.0% |
|
| 7.667725750558191 |
1 |
0.0% |
|
| 7.692208543567821 |
1 |
0.0% |
|
| 7.754598748054839 |
1 |
0.0% |
|
| 10.5267660517847 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
3.4823e-15 |
| Minimum |
-4.4989 |
| Maximum |
8.8777 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-4.4989 |
| 5-th percentile |
-1.5932 |
| Q1 |
-0.58288 |
| Median |
0.048072 |
| Q3 |
0.64882 |
| 95-th percentile |
1.3731 |
| Maximum |
8.8777 |
| Range |
13.377 |
| Interquartile range |
1.2317 |
Descriptive statistics
| Standard deviation |
0.91532 |
| Coef of variation |
262850000000000 |
| Kurtosis |
0.28477 |
| Mean |
3.4823e-15 |
| MAD |
0.72734 |
| Skewness |
-0.30842 |
| Sum |
1.3993e-09 |
| Variance |
0.8378 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 1.2752570390934999 |
77 |
0.0% |
|
| 1.1241469228868501 |
77 |
0.0% |
|
| 0.271956610213985 |
62 |
0.0% |
|
| 1.44662697638966 |
60 |
0.0% |
|
| 0.5838968102925071 |
53 |
0.0% |
|
| 0.38872408312047796 |
48 |
0.0% |
|
| 1.157633713505 |
45 |
0.0% |
|
| 1.46891114338139 |
40 |
0.0% |
|
| 1.1285389817093798 |
39 |
0.0% |
|
| 1.2452765300023998 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -4.49894467676621 |
1 |
0.0% |
|
| -4.39130706780494 |
1 |
0.0% |
|
| -4.19932124976578 |
1 |
0.0% |
|
| -4.19661969463528 |
1 |
0.0% |
|
| -4.15253175950472 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 5.685899051594321 |
1 |
0.0% |
|
| 5.720478632456981 |
1 |
0.0% |
|
| 5.7845138896294594 |
1 |
0.0% |
|
| 5.82565431863365 |
1 |
0.0% |
|
| 8.87774159774277 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
1.392e-15 |
| Minimum |
-14.13 |
| Maximum |
17.315 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-14.13 |
| 5-th percentile |
-1.4917 |
| Q1 |
-0.46804 |
| Median |
0.066413 |
| Q3 |
0.5233 |
| 95-th percentile |
1.3253 |
| Maximum |
17.315 |
| Range |
31.445 |
| Interquartile range |
0.99133 |
Descriptive statistics
| Standard deviation |
0.87625 |
| Coef of variation |
629490000000000 |
| Kurtosis |
10.419 |
| Mean |
1.392e-15 |
| MAD |
0.64782 |
| Skewness |
-1.101 |
| Sum |
4.0946e-1 |
| Variance |
0.76782 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.34246975411076896 |
77 |
0.0% |
|
| -0.37196212502841897 |
77 |
0.0% |
|
| 0.318688063430157 |
62 |
0.0% |
|
| -0.12182037858308699 |
60 |
0.0% |
|
| 0.17867583647653199 |
53 |
0.0% |
|
| 0.23207137768386 |
48 |
0.0% |
|
| 0.878174917750572 |
45 |
0.0% |
|
| -0.0297415143257285 |
40 |
0.0% |
|
| 0.7865060536879019 |
39 |
0.0% |
|
| -0.255230524748655 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -14.1298545174931 |
1 |
0.0% |
|
| -13.5632729563133 |
1 |
0.0% |
|
| -13.30388757707 |
1 |
0.0% |
|
| -13.2568330912778 |
1 |
0.0% |
|
| -13.2515419788937 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 6.35185349844491 |
1 |
0.0% |
|
| 6.44279790144451 |
1 |
0.0% |
|
| 7.05913181057395 |
1 |
0.0% |
|
| 8.289889559546191 |
1 |
0.0% |
|
| 17.315111517627802 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-7.5285e-16 |
| Minimum |
-25.163 |
| Maximum |
9.2535 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-25.163 |
| 5-th percentile |
-0.983 |
| Q1 |
-0.48375 |
| Median |
-0.065676 |
| Q3 |
0.39967 |
| 95-th percentile |
1.2746 |
| Maximum |
9.2535 |
| Range |
34.416 |
| Interquartile range |
0.88342 |
Descriptive statistics
| Standard deviation |
0.84934 |
| Coef of variation |
-1128200000000000 |
| Kurtosis |
94.8 |
| Mean |
-7.5285e-16 |
| MAD |
0.56387 |
| Skewness |
-3.8449 |
| Sum |
-1.0823e-1 |
| Variance |
0.72137 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.6019568028284449 |
77 |
0.0% |
|
| -0.37465644005137605 |
77 |
0.0% |
|
| 0.549365128729473 |
62 |
0.0% |
|
| -0.651405237009102 |
60 |
0.0% |
|
| 0.47389827829767206 |
53 |
0.0% |
|
| 2.12502188299054 |
48 |
0.0% |
|
| 0.536917519702814 |
45 |
0.0% |
|
| 3.6645884808692504 |
40 |
0.0% |
|
| 0.31643526103505604 |
39 |
0.0% |
|
| -1.07208498526811 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -25.162799369324798 |
1 |
0.0% |
|
| -24.019098547590197 |
1 |
0.0% |
|
| -23.8156358284126 |
1 |
0.0% |
|
| -23.2415971479491 |
1 |
0.0% |
|
| -22.8839985767803 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 7.766636362866991 |
1 |
0.0% |
|
| 7.89339253241379 |
1 |
0.0% |
|
| 8.538195138626161 |
1 |
0.0% |
|
| 9.20705853529557 |
1 |
0.0% |
|
| 9.25352625047285 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
4.3288e-16 |
| Minimum |
-9.4987 |
| Maximum |
5.0411 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-9.4987 |
| 5-th percentile |
-1.3581 |
| Q1 |
-0.49885 |
| Median |
-0.0036363 |
| Q3 |
0.50081 |
| 95-th percentile |
1.3944 |
| Maximum |
5.0411 |
| Range |
14.54 |
| Interquartile range |
0.99966 |
Descriptive statistics
| Standard deviation |
0.83818 |
| Coef of variation |
1936300000000000 |
| Kurtosis |
2.5783 |
| Mean |
4.3288e-16 |
| MAD |
0.63582 |
| Skewness |
-0.25988 |
| Sum |
2.7262e-1 |
| Variance |
0.70254 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.43899243243668296 |
77 |
0.0% |
|
| -0.0526401462570187 |
77 |
0.0% |
|
| -0.25778585794493303 |
62 |
0.0% |
|
| 0.6179704765287819 |
60 |
0.0% |
|
| -0.49884979866504103 |
53 |
0.0% |
|
| 0.40554867355562896 |
48 |
0.0% |
|
| 0.712873012618197 |
45 |
0.0% |
|
| -0.105189588790714 |
40 |
0.0% |
|
| 0.587856253020328 |
39 |
0.0% |
|
| -0.0686980996025901 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -9.498745921046769 |
1 |
0.0% |
|
| -9.33519307905321 |
1 |
0.0% |
|
| -9.287832213974019 |
1 |
0.0% |
|
| -9.264608732956551 |
1 |
0.0% |
|
| -9.17055721888169 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 4.19959110679305 |
1 |
0.0% |
|
| 4.24384121345385 |
1 |
0.0% |
|
| 4.2956482344645 |
1 |
0.0% |
|
| 4.71239756635225 |
1 |
0.0% |
|
| 5.04106918541184 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
9.0497e-16 |
| Minimum |
-7.2135 |
| Maximum |
5.592 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-7.2135 |
| 5-th percentile |
-1.3563 |
| Q1 |
-0.4563 |
| Median |
0.0037348 |
| Q3 |
0.45895 |
| 95-th percentile |
1.2862 |
| Maximum |
5.592 |
| Range |
12.805 |
| Interquartile range |
0.91525 |
Descriptive statistics
| Standard deviation |
0.81404 |
| Coef of variation |
899520000000000 |
| Kurtosis |
1.725 |
| Mean |
9.0497e-16 |
| MAD |
0.60579 |
| Skewness |
0.10919 |
| Sum |
2.9615e-1 |
| Variance |
0.66266 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.116090785002835 |
77 |
0.0% |
|
| -0.33059044844294394 |
77 |
0.0% |
|
| 0.0162561279842771 |
62 |
0.0% |
|
| 0.927600044556072 |
60 |
0.0% |
|
| -0.14009868476221 |
53 |
0.0% |
|
| -0.440929511947803 |
48 |
0.0% |
|
| 0.00677355522536129 |
45 |
0.0% |
|
| -2.0979443214639 |
40 |
0.0% |
|
| 0.0493500831769145 |
39 |
0.0% |
|
| 0.255267674459398 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -7.21352743017759 |
1 |
0.0% |
|
| -6.93829731768481 |
1 |
0.0% |
|
| -4.93273305547833 |
1 |
0.0% |
|
| -4.676092279153361 |
1 |
0.0% |
|
| -4.619034341772441 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 4.8910624409520995 |
1 |
0.0% |
|
| 5.2283417900513 |
1 |
0.0% |
|
| 5.5017472139665 |
1 |
0.0% |
|
| 5.572113326879691 |
1 |
0.0% |
|
| 5.59197142733558 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
5.0855e-16 |
| Minimum |
-54.498 |
| Maximum |
39.421 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-54.498 |
| 5-th percentile |
-0.55843 |
| Q1 |
-0.21172 |
| Median |
-0.062481 |
| Q3 |
0.13304 |
| 95-th percentile |
0.83614 |
| Maximum |
39.421 |
| Range |
93.919 |
| Interquartile range |
0.34476 |
Descriptive statistics
| Standard deviation |
0.77093 |
| Coef of variation |
1515900000000000 |
| Kurtosis |
271.02 |
| Mean |
5.0855e-16 |
| MAD |
0.34191 |
| Skewness |
-2.0372 |
| Sum |
1.8247e-1 |
| Variance |
0.59433 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.18037011855969298 |
77 |
0.0% |
|
| -0.132079724302295 |
77 |
0.0% |
|
| -0.187420788431655 |
62 |
0.0% |
|
| 0.0057566554189328704 |
60 |
0.0% |
|
| -0.12071403428047302 |
53 |
0.0% |
|
| -0.0869893297425326 |
48 |
0.0% |
|
| 0.0536071193018422 |
45 |
0.0% |
|
| -0.167555416292594 |
40 |
0.0% |
|
| 0.0452174411898587 |
39 |
0.0% |
|
| 0.0169521541786674 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -54.497720494566 |
1 |
0.0% |
|
| -28.009635333749 |
1 |
0.0% |
|
| -25.222345240529698 |
1 |
0.0% |
|
| -23.646890332167303 |
1 |
0.0% |
|
| -23.4201725720228 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 23.649094568125502 |
1 |
0.0% |
|
| 24.1338941917421 |
1 |
0.0% |
|
| 26.237390789565897 |
1 |
0.0% |
|
| 38.1172091261285 |
1 |
0.0% |
|
| 39.4209042482199 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
1.5373e-16 |
| Minimum |
-34.83 |
| Maximum |
27.203 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-34.83 |
| 5-th percentile |
-0.50467 |
| Q1 |
-0.22839 |
| Median |
-0.02945 |
| Q3 |
0.18638 |
| 95-th percentile |
0.53787 |
| Maximum |
27.203 |
| Range |
62.033 |
| Interquartile range |
0.41477 |
Descriptive statistics
| Standard deviation |
0.73452 |
| Coef of variation |
4778000000000000 |
| Kurtosis |
207.29 |
| Mean |
1.5373e-16 |
| MAD |
0.31907 |
| Skewness |
3.593 |
| Sum |
4.718e-11 |
| Variance |
0.53953 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.26258084604117604 |
77 |
0.0% |
|
| 0.26976495136135703 |
77 |
0.0% |
|
| -0.36115803659984497 |
62 |
0.0% |
|
| -0.0642082814806287 |
60 |
0.0% |
|
| -0.35233380052375 |
53 |
0.0% |
|
| -0.0672166613423604 |
48 |
0.0% |
|
| -0.20743240447289701 |
45 |
0.0% |
|
| -0.0402375927503545 |
40 |
0.0% |
|
| -0.191819982814025 |
39 |
0.0% |
|
| 0.0073428026657956095 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -34.8303821448146 |
1 |
0.0% |
|
| -22.889347040939 |
1 |
0.0% |
|
| -22.797603905551895 |
1 |
0.0% |
|
| -22.7575398590576 |
1 |
0.0% |
|
| -22.665684604861497 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 22.5806752741477 |
1 |
0.0% |
|
| 22.5889894712903 |
1 |
0.0% |
|
| 22.5995433627945 |
1 |
0.0% |
|
| 22.614889367616897 |
1 |
0.0% |
|
| 27.2028391573154 |
6 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
7.9599e-16 |
| Minimum |
-10.933 |
| Maximum |
10.503 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-10.933 |
| 5-th percentile |
-1.0819 |
| Q1 |
-0.54235 |
| Median |
0.0067819 |
| Q3 |
0.52855 |
| 95-th percentile |
1.129 |
| Maximum |
10.503 |
| Range |
21.436 |
| Interquartile range |
1.0709 |
Descriptive statistics
| Standard deviation |
0.7257 |
| Coef of variation |
911700000000000 |
| Kurtosis |
2.833 |
| Mean |
7.9599e-16 |
| MAD |
0.58421 |
| Skewness |
-0.21326 |
| Sum |
-9.8112e-11 |
| Variance |
0.52664 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.8162637631578471 |
77 |
0.0% |
|
| 0.8446266467757121 |
77 |
0.0% |
|
| -0.984261949244254 |
62 |
0.0% |
|
| -0.0805870774450856 |
60 |
0.0% |
|
| -0.9969367748280931 |
53 |
0.0% |
|
| -0.0726415994946915 |
48 |
0.0% |
|
| -0.6924166841818179 |
45 |
0.0% |
|
| 0.0961715739635631 |
40 |
0.0% |
|
| -0.650117795537897 |
39 |
0.0% |
|
| 0.250885695089417 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -10.933143697655 |
1 |
0.0% |
|
| -9.49942296430251 |
1 |
0.0% |
|
| -8.88701714094871 |
6 |
0.0% |
|
| -8.59364156538624 |
1 |
0.0% |
|
| -8.555807930456341 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 7.357255161770509 |
1 |
0.0% |
|
| 8.27223298396612 |
1 |
0.0% |
|
| 8.316275438913571 |
1 |
0.0% |
|
| 8.361985191684349 |
1 |
0.0% |
|
| 10.5030900899454 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
5.3676e-16 |
| Minimum |
-44.808 |
| Maximum |
22.528 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-44.808 |
| 5-th percentile |
-0.47225 |
| Q1 |
-0.16185 |
| Median |
-0.011193 |
| Q3 |
0.14764 |
| 95-th percentile |
0.48802 |
| Maximum |
22.528 |
| Range |
67.336 |
| Interquartile range |
0.30949 |
Descriptive statistics
| Standard deviation |
0.62446 |
| Coef of variation |
1163400000000000 |
| Kurtosis |
440.09 |
| Mean |
5.3676e-16 |
| MAD |
0.26194 |
| Skewness |
-5.8751 |
| Sum |
7.3442e-11 |
| Variance |
0.38995 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.14030430201432598 |
77 |
0.0% |
|
| 0.0206746676928111 |
77 |
0.0% |
|
| 0.354198094344309 |
62 |
0.0% |
|
| -0.0729910792746877 |
60 |
0.0% |
|
| 0.36348490597863004 |
53 |
0.0% |
|
| -0.0365842826760227 |
48 |
0.0% |
|
| -0.11859751164434901 |
45 |
0.0% |
|
| -0.0925489695836041 |
40 |
0.0% |
|
| -0.11406946378171699 |
39 |
0.0% |
|
| 0.10379660601100901 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -44.807735203791296 |
1 |
0.0% |
|
| -36.666000066027 |
1 |
0.0% |
|
| -32.828994997462004 |
1 |
0.0% |
|
| -30.269720014317002 |
1 |
0.0% |
|
| -27.533643285000302 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 19.002941823292698 |
1 |
0.0% |
|
| 19.228169082574198 |
1 |
0.0% |
|
| 20.8033440994696 |
1 |
0.0% |
|
| 22.0835448685737 |
1 |
0.0% |
|
| 22.5284116897749 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
4.4581e-15 |
| Minimum |
-2.8366 |
| Maximum |
4.5845 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-2.8366 |
| 5-th percentile |
-1.1437 |
| Q1 |
-0.35459 |
| Median |
0.040976 |
| Q3 |
0.43953 |
| 95-th percentile |
0.86636 |
| Maximum |
4.5845 |
| Range |
7.4212 |
| Interquartile range |
0.79411 |
Descriptive statistics
| Standard deviation |
0.60565 |
| Coef of variation |
135850000000000 |
| Kurtosis |
0.61887 |
| Mean |
4.4581e-15 |
| MAD |
0.46844 |
| Skewness |
-0.5525 |
| Sum |
1.2736e-09 |
| Variance |
0.36681 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.726211883811499 |
77 |
0.0% |
|
| 0.3578272492998061 |
77 |
0.0% |
|
| 0.6207093385008 |
62 |
0.0% |
|
| 1.01813597043583 |
60 |
0.0% |
|
| 0.6048265697520401 |
53 |
0.0% |
|
| 0.529692767553245 |
48 |
0.0% |
|
| 0.8914796678605641 |
45 |
0.0% |
|
| -1.34566370602836 |
40 |
0.0% |
|
| 0.9159355995388021 |
39 |
0.0% |
|
| 1.00995227965779 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -2.83662691870341 |
1 |
0.0% |
|
| -2.82484890293617 |
1 |
0.0% |
|
| -2.82268359235889 |
1 |
0.0% |
|
| -2.82238396858124 |
1 |
0.0% |
|
| -2.81489763570598 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 3.9982936780756897 |
1 |
0.0% |
|
| 4.014444384730609 |
1 |
0.0% |
|
| 4.01634181669268 |
1 |
0.0% |
|
| 4.02286589044732 |
1 |
0.0% |
|
| 4.58454913689817 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
1.453e-15 |
| Minimum |
-10.295 |
| Maximum |
7.5196 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-10.295 |
| 5-th percentile |
-0.82503 |
| Q1 |
-0.31715 |
| Median |
0.016594 |
| Q3 |
0.35072 |
| 95-th percentile |
0.7607 |
| Maximum |
7.5196 |
| Range |
17.815 |
| Interquartile range |
0.66786 |
Descriptive statistics
| Standard deviation |
0.52128 |
| Coef of variation |
358760000000000 |
| Kurtosis |
4.2904 |
| Mean |
1.453e-15 |
| MAD |
0.40326 |
| Skewness |
-0.41579 |
| Sum |
1.5211e-1 |
| Variance |
0.27173 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.18642294572338897 |
77 |
0.0% |
|
| 0.36662430700491294 |
77 |
0.0% |
|
| -0.29713787612847997 |
62 |
0.0% |
|
| 0.6635747724804879 |
60 |
0.0% |
|
| -0.26455958625151 |
53 |
0.0% |
|
| 0.41468514197751 |
48 |
0.0% |
|
| 0.7302403643301479 |
45 |
0.0% |
|
| 0.510304957067478 |
40 |
0.0% |
|
| 0.7300730401400359 |
39 |
0.0% |
|
| 0.369398160051982 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -10.2953970749851 |
1 |
0.0% |
|
| -8.69662677026752 |
1 |
0.0% |
|
| -7.495741104057091 |
1 |
0.0% |
|
| -7.0813253463773895 |
1 |
0.0% |
|
| -7.02578318190186 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 5.54159759459217 |
1 |
0.0% |
|
| 5.8261590349735 |
1 |
0.0% |
|
| 5.8524835709145595 |
1 |
0.0% |
|
| 6.07085038407798 |
1 |
0.0% |
|
| 7.51958867870916 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
1.6991e-15 |
| Minimum |
-2.6046 |
| Maximum |
3.5173 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-2.6046 |
| 5-th percentile |
-0.69735 |
| Q1 |
-0.32698 |
| Median |
-0.052139 |
| Q3 |
0.24095 |
| 95-th percentile |
0.92092 |
| Maximum |
3.5173 |
| Range |
6.1219 |
| Interquartile range |
0.56794 |
Descriptive statistics
| Standard deviation |
0.48223 |
| Coef of variation |
283810000000000 |
| Kurtosis |
0.91901 |
| Mean |
1.6991e-15 |
| MAD |
0.37663 |
| Skewness |
0.57669 |
| Sum |
4.805e-1 |
| Variance |
0.23254 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| -0.39882751495946295 |
77 |
0.0% |
|
| 0.0965444707905616 |
77 |
0.0% |
|
| 0.16673563433513197 |
62 |
0.0% |
|
| -0.671322844293718 |
60 |
0.0% |
|
| 0.21967064744260398 |
53 |
0.0% |
|
| 0.73586965178554 |
48 |
0.0% |
|
| 0.384013445762976 |
45 |
0.0% |
|
| -0.18267352250172897 |
40 |
0.0% |
|
| 0.38387941757557303 |
39 |
0.0% |
|
| 0.110373548574965 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -2.60455055280817 |
1 |
0.0% |
|
| -2.53432972105675 |
1 |
0.0% |
|
| -2.2416202900029503 |
1 |
0.0% |
|
| -2.06856086855144 |
1 |
0.0% |
|
| -1.8553553377608 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 3.15532747327538 |
1 |
0.0% |
|
| 3.22017837466898 |
1 |
0.0% |
|
| 3.41563624349633 |
1 |
0.0% |
|
| 3.4632456536447997 |
1 |
0.0% |
|
| 3.5173456116237998 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-3.6602e-16 |
| Minimum |
-22.566 |
| Maximum |
31.612 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-22.566 |
| 5-th percentile |
-0.41525 |
| Q1 |
-0.07084 |
| Median |
0.0013421 |
| Q3 |
0.091045 |
| 95-th percentile |
0.38775 |
| Maximum |
31.612 |
| Range |
54.178 |
| Interquartile range |
0.16188 |
Descriptive statistics
| Standard deviation |
0.40363 |
| Coef of variation |
-1102800000000000 |
| Kurtosis |
244.99 |
| Mean |
-3.6602e-16 |
| MAD |
0.18147 |
| Skewness |
-1.1702 |
| Sum |
-1.0442e-1 |
| Variance |
0.16292 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.0277351215052822 |
77 |
0.0% |
|
| -0.035866315294695 |
77 |
0.0% |
|
| -0.0682990099344722 |
62 |
0.0% |
|
| 0.0968009452278396 |
60 |
0.0% |
|
| -0.0392094515896982 |
53 |
0.0% |
|
| -0.0582327676516994 |
48 |
0.0% |
|
| -0.0284652724675567 |
45 |
0.0% |
|
| 0.107058302469808 |
40 |
0.0% |
|
| -0.0319023040878611 |
39 |
0.0% |
|
| -0.0283020664307734 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -22.5656793207827 |
1 |
0.0% |
|
| -9.89524404755692 |
1 |
0.0% |
|
| -9.845807692778981 |
1 |
0.0% |
|
| -9.793567905137511 |
1 |
0.0% |
|
| -9.544855375391482 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 10.135597346295699 |
1 |
0.0% |
|
| 10.507884353083499 |
1 |
0.0% |
|
| 11.135739844574198 |
1 |
0.0% |
|
| 12.1524011068287 |
1 |
0.0% |
|
| 31.612198106136304 |
1 |
0.0% |
|
| Distinct count |
275663 |
| Unique (%) |
96.8% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
-1.206e-16 |
| Minimum |
-15.43 |
| Maximum |
33.848 |
| Zeros (%) |
0.0% |

Quantile statistics
| Minimum |
-15.43 |
| 5-th percentile |
-0.31784 |
| Q1 |
-0.05296 |
| Median |
0.011244 |
| Q3 |
0.07828 |
| 95-th percentile |
0.25609 |
| Maximum |
33.848 |
| Range |
49.278 |
| Interquartile range |
0.13124 |
Descriptive statistics
| Standard deviation |
0.33008 |
| Coef of variation |
-2736900000000000 |
| Kurtosis |
933.4 |
| Mean |
-1.206e-16 |
| MAD |
0.12933 |
| Skewness |
11.192 |
| Sum |
-3.4758e-11 |
| Variance |
0.10895 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 0.0184945729704665 |
77 |
0.0% |
|
| -0.0602821510762213 |
77 |
0.0% |
|
| -0.0295847028396107 |
62 |
0.0% |
|
| 0.0286968782920849 |
60 |
0.0% |
|
| -0.0427869554036275 |
53 |
0.0% |
|
| -0.0266576195050194 |
48 |
0.0% |
|
| 0.0361233094119335 |
45 |
0.0% |
|
| 0.0718180029478637 |
40 |
0.0% |
|
| 0.0298493414012052 |
39 |
0.0% |
|
| -0.0203586378568534 |
36 |
0.0% |
|
| Other values (275653) |
284270 |
99.8% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| -15.430083905534898 |
1 |
0.0% |
|
| -11.710895639451499 |
1 |
0.0% |
|
| -9.617915452382391 |
1 |
0.0% |
|
| -8.65656990038166 |
1 |
0.0% |
|
| -8.47868564330279 |
1 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 15.870474054688598 |
1 |
0.0% |
|
| 15.942150981273501 |
1 |
0.0% |
|
| 16.1296091387323 |
1 |
0.0% |
|
| 22.620072218580297 |
1 |
0.0% |
|
| 33.8478078188831 |
1 |
0.0% |
|
| Distinct count |
32767 |
| Unique (%) |
11.5% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |
| Infinite (%) |
0.0% |
| Infinite (n) |
0 |
| Mean |
88.35 |
| Minimum |
0 |
| Maximum |
25691 |
| Zeros (%) |
0.6% |
Quantile statistics
| Minimum |
0 |
| 5-th percentile |
0.92 |
| Q1 |
5.6 |
| Median |
22 |
| Q3 |
77.165 |
| 95-th percentile |
365 |
| Maximum |
25691 |
| Range |
25691 |
| Interquartile range |
71.565 |
Descriptive statistics
| Standard deviation |
250.12 |
| Coef of variation |
2.831 |
| Kurtosis |
845.09 |
| Mean |
88.35 |
| MAD |
103.53 |
| Skewness |
16.978 |
| Sum |
25163000 |
| Variance |
62560 |
| Memory size |
2.2 MiB |
| Value |
Count |
Frequency (%) |
|
| 1.0 |
13688 |
4.8% |
|
| 1.98 |
6044 |
2.1% |
|
| 0.89 |
4872 |
1.7% |
|
| 9.99 |
4747 |
1.7% |
|
| 15.0 |
3280 |
1.2% |
|
| 0.76 |
2998 |
1.1% |
|
| 10.0 |
2950 |
1.0% |
|
| 1.29 |
2892 |
1.0% |
|
| 1.79 |
2623 |
0.9% |
|
| 0.99 |
2304 |
0.8% |
|
| Other values (32757) |
238409 |
83.7% |
|
Minimum 5 values
| Value |
Count |
Frequency (%) |
|
| 0.0 |
1825 |
0.6% |
|
| 0.01 |
718 |
0.3% |
|
| 0.02 |
85 |
0.0% |
|
| 0.03 |
3 |
0.0% |
|
| 0.04 |
11 |
0.0% |
|
Maximum 5 values
| Value |
Count |
Frequency (%) |
|
| 11898.09 |
1 |
0.0% |
|
| 12910.93 |
1 |
0.0% |
|
| 18910.0 |
1 |
0.0% |
|
| 19656.53 |
1 |
0.0% |
|
| 25691.16 |
1 |
0.0% |
|
| Distinct count |
2 |
| Unique (%) |
0.0% |
| Missing (%) |
0.0% |
| Missing (n) |
0 |


|
Time |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
V10 |
V11 |
V12 |
V13 |
V14 |
V15 |
V16 |
V17 |
V18 |
V19 |
V20 |
V21 |
V22 |
V23 |
V24 |
V25 |
V26 |
V27 |
V28 |
Amount |
Class |
| 0 |
0.0 |
-1.359807 |
-0.072781 |
2.536347 |
1.378155 |
-0.338321 |
0.462388 |
0.239599 |
0.098698 |
0.363787 |
0.090794 |
-0.551600 |
-0.617801 |
-0.991390 |
-0.311169 |
1.468177 |
-0.470401 |
0.207971 |
0.025791 |
0.403993 |
0.251412 |
-0.018307 |
0.277838 |
-0.110474 |
0.066928 |
0.128539 |
-0.189115 |
0.133558 |
-0.021053 |
149.62 |
0 |
| 1 |
0.0 |
1.191857 |
0.266151 |
0.166480 |
0.448154 |
0.060018 |
-0.082361 |
-0.078803 |
0.085102 |
-0.255425 |
-0.166974 |
1.612727 |
1.065235 |
0.489095 |
-0.143772 |
0.635558 |
0.463917 |
-0.114805 |
-0.183361 |
-0.145783 |
-0.069083 |
-0.225775 |
-0.638672 |
0.101288 |
-0.339846 |
0.167170 |
0.125895 |
-0.008983 |
0.014724 |
2.69 |
0 |
| 2 |
1.0 |
-1.358354 |
-1.340163 |
1.773209 |
0.379780 |
-0.503198 |
1.800499 |
0.791461 |
0.247676 |
-1.514654 |
0.207643 |
0.624501 |
0.066084 |
0.717293 |
-0.165946 |
2.345865 |
-2.890083 |
1.109969 |
-0.121359 |
-2.261857 |
0.524980 |
0.247998 |
0.771679 |
0.909412 |
-0.689281 |
-0.327642 |
-0.139097 |
-0.055353 |
-0.059752 |
378.66 |
0 |
| 3 |
1.0 |
-0.966272 |
-0.185226 |
1.792993 |
-0.863291 |
-0.010309 |
1.247203 |
0.237609 |
0.377436 |
-1.387024 |
-0.054952 |
-0.226487 |
0.178228 |
0.507757 |
-0.287924 |
-0.631418 |
-1.059647 |
-0.684093 |
1.965775 |
-1.232622 |
-0.208038 |
-0.108300 |
0.005274 |
-0.190321 |
-1.175575 |
0.647376 |
-0.221929 |
0.062723 |
0.061458 |
123.50 |
0 |
| 4 |
2.0 |
-1.158233 |
0.877737 |
1.548718 |
0.403034 |
-0.407193 |
0.095921 |
0.592941 |
-0.270533 |
0.817739 |
0.753074 |
-0.822843 |
0.538196 |
1.345852 |
-1.119670 |
0.175121 |
-0.451449 |
-0.237033 |
-0.038195 |
0.803487 |
0.408542 |
-0.009431 |
0.798278 |
-0.137458 |
0.141267 |
-0.206010 |
0.502292 |
0.219422 |
0.215153 |
69.99 |
0 |
The function below is used to calculate the various evaluation metrics including area under the ROC curve, the area under the precision-recall curve,-f1-score etc.
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import precision_recall_fscore_support
from numpy import trapz
from scipy.integrate import simps
from sklearn.metrics import f1_score
def Evaluate(labels, predictions, p=0.5):
CM= confusion_matrix(labels, predictions > p)
TN = CM[0][0]
FN = CM[1][0]
TP = CM[1][1]
FP = CM[0][1]
print('Legitimate Transactions Detected (True Negatives): {}'.format(TN))
print('Fraudulent Transactions Missed (False Negatives): {}'.format(FN))
print('Fraudulent Transactions Detected (True Positives): {}'.format(TP))
print('Legitimate Transactions Incorrectly Detected (False Positives):{}'.format(FP))
print('Total Fraudulent Transactions: ', np.sum(CM[1]))
auc = roc_auc_score(labels, predictions)
prec=precision_score(labels, predictions>0.5)
rec=recall_score(labels, predictions>0.5)
# calculate F1 score
f1 = f1_score(labels, predictions>p)
print('auc :{}'.format(auc))
print('precision :{}'.format(prec))
print('recall :{}'.format(rec))
print('f1 :{}'.format(f1))
# Compute Precision-Recall and plot curve
precision, recall, thresholds = precision_recall_curve(labels, predictions >0.5)
#use the trapezoidal rule to calculate the area under the precion-recall curve
area = trapz(recall, precision)
#area = simps(recall, precision)
print("Area Under Precision Recall Curve(AP): %0.4f" % area) #should be same as AP?
from sklearn.metrics import auc
We will attempt to investigate the performance of several ML algorithms on imbalanced target class data classification. The xgboost algorithm will be used to model data that is undersampled, no sample at all, Synthetic Minority Oversampling Technique and also modified to perform a cost sensitive learning. The other ML algorithms which will be tested include Forest of Randomized Trees, RusBoost, EasyEnsemble and Bagging classifier. The cost-sensitive xgboost method will invlove experimental determining the optimal weight on the minority target class using bayesian optimization.
XGBoost No Weights
The first model considered here is an xgboost with default hyperparameter values with no sampling of data.
xgb_no_weights = clf.fit(X=train_x, y=train_y)
#xgb_no_weights_pred = xgb_no_weights.predict_proba(test_x)
xgb_no_weights_pred = xgb_no_weights.predict_proba(test_x)[:,1]
dump(xgb_no_weights, '/content/drive/My Drive/ImbalancedData/xgb_no_weights.joblib')
Evaluate(labels=test_y, predictions=xgb_no_weights_pred, p=0.5)
Legitimate Transactions Detected (True Negatives): 56854
Fraudulent Transactions Missed (False Negatives): 26
Fraudulent Transactions Detected (True Positives): 79
Legitimate Transactions Incorrectly Detected (False Positives):3
Total Fraudulent Transactions: 105
auc :0.9777749860343032
precision :0.9634146341463414
recall :0.7523809523809524
f1 :0.8449197860962566
Area Under Precision Recall Curve(AP): 0.8563
xgb_no_weights = load( '/content/drive/My Drive/ImbalancedData/xgb_no_weights.joblib')
xgb_no_weights_pred = xgb_no_weights.predict_proba(test_x)[:,1]
#Evaluate(labels=test_y, predictions=xgb_no_weights_pred, p=0.5)
Convert these vectors from python to R vectors. This will alow to use the R library for evaluating ML models /MLmetrics to be used in finding area under the precision-recall curve.
#%%R -i xgb_no_weights_pred
#library( MLmetrics)
#library(yardstick)
#library(mltools)
#library("glue")
#MLmetrics::AUC(xgb_no_weights_pred,test_y)
#d= data.frame(pred=xgb_no_weights_pred[,2],truth=as.factor(test_y))
#glue("Test Set : Area Under Precision-Recall Curve: {yardstick::pr_auc(d, truth, pred)}")
#glue("Test Set : Area Under Precision-Recall Curve: {MLmetrics::PRAUC(as.vector(xgb_no_weights_pred),test_y)}")
#head(d)
dump(xgb_no_weights, '/content/drive/My Drive/ImbalancedData/xgb_no_weights.joblib')
['/content/drive/My Drive/ImbalancedData/xgb_no_weights.joblib']
Model one : XGBoost with Weights on Label/ No Sampling
ns_model = bayessearch.fit(X=train_x, y=train_y)
os.getcwd()
#ns_model
dump(ns_model, '/content/drive/My Drive/ImbalancedData/ns_model.joblib')
['/content/drive/My Drive/ImbalancedData/ns_model.joblib']
#dump(ns_model, '/content/drive/My Drive/ImbalancedData/ns_model.joblib')
ns_model = load('/content/drive/My Drive/ImbalancedData/ns_model.joblib')
ns_model_pred = ns_model.predict_proba(test_x)[:,1]
Evaluate(labels=test_y, predictions=ns_model_pred, p=0.5)
Legitimate Transactions Detected (True Negatives): 56839
Fraudulent Transactions Missed (False Negatives): 15
Fraudulent Transactions Detected (True Positives): 90
Legitimate Transactions Incorrectly Detected (False Positives):18
Total Fraudulent Transactions: 105
auc :0.9961524191434317
precision :0.8333333333333334
recall :0.8571428571428571
f1 :0.8450704225352113
Area Under PR Curve(AP): 0.8435
XGBoost with Undersampling
from collections import Counter
from sklearn.datasets import make_classification
from imblearn.under_sampling import RandomUnderSampler # doctest: +NORMALIZE_WHITESPACE
rus = RandomUnderSampler(random_state=42)
X_rus, y_rus = rus.fit_resample(X=train_x, y=train_y)
print('Resampled dataset shape %s' % Counter(y_rus))
xgb_model_rus = clf.fit(X=X_rus, y=y_rus)
dump(xgb_model_rus, '/content/drive/My Drive/ImbalancedData/xgb_model_rus.joblib')
Resampled dataset shape Counter({0: 402, 1: 402})
['/content/drive/My Drive/ImbalancedData/xgb_model_rus.joblib']
xgb_model_rus = load('/content/drive/My Drive/ImbalancedData/xgb_model_rus.joblib')
p=0.5
xgb_model_rus_pred = xgb_model_rus.predict_proba(test_x.values)[:,1]
#predict_proba(test_x)[:,1]
print(" balanced_accuracy_score {}".format(balanced_accuracy_score(test_y, xgb_model_rus_pred>p) ))
cm=confusion_matrix(test_y, xgb_model_rus_pred>0.5)
print("confusion matrix : {}".format(cm))
#test_x.columns
#xgb_model_rus.
Evaluate(labels=test_y, predictions=xgb_model_rus_pred, p=0.5)
import collections
counter=collections.Counter(xgb_model_rus_pred>0.5)
print(counter)
balanced_accuracy_score 0.9634347489985318
confusion matrix : [[54865 1992]
[ 4 101]]
Legitimate Transactions Detected (True Negatives): 54865
Fraudulent Transactions Missed (False Negatives): 4
Fraudulent Transactions Detected (True Positives): 101
Legitimate Transactions Incorrectly Detected (False Positives):1992
Total Fraudulent Transactions: 105
auc :0.9926581055061278
precision :0.0482560917343526
recall :0.9619047619047619
f1 :0.09190172884440401
Area Under PR Curve(AP): 0.5033
Counter({False: 54869, True: 2093})
print("Classification Report")
print(classification_report(test_y, xgb_model_rus_pred > p))
# ROC curve and Area-Under-Curve (AUC)
#calculating accuracy
accuracy_xgbm_sm= accuracy_score(test_y, xgb_model_rus_pred>p)
print('accuracy score : {:0.3f}'.format( accuracy_xgbm_sm))
roc_auc_sm = roc_auc_score(test_y, xgb_model_rus_pred)
print('roc score : {:0.3f}'.format( roc_auc_sm))
Classification Report
precision recall f1-score support
0 1.00 0.96 0.98 56857
1 0.05 0.96 0.09 105
accuracy 0.96 56962
macro avg 0.52 0.96 0.54 56962
weighted avg 1.00 0.96 0.98 56962
accuracy score : 0.965
roc score : 0.993
SMOTE
from collections import Counter
from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE # doctest: +NORMALIZE_WHITESPACE
print('Original dataset shape %s' % Counter(train_y))
sm = SMOTE(random_state=42)
X_res, y_res = sm.fit_resample(X=train_x, y=train_y)
print('Resampled dataset shape %s' % Counter(y_res))
xgb_model_sm= clf.fit(X=X_res, y=y_res)
xgb_model_sm_pred = xgb_model_sm.predict(test_x.values)
#iba(y_test, y_pred)
#balanced_accuracy_score(y_test, y_pred)
cm=confusion_matrix(test_y, xgb_model_sm_pred)
print("confusion matrix")
print(cm)
print("Classification Report")
print(classification_report(test_y, xgb_model_sm_pred))
# ROC curve and Area-Under-Curve (AUC)
#calculating accuracy
accuracy_xgbm_sm= accuracy_score(test_y, xgb_model_sm_pred)
print('accuracy score : {:0.3f}'.format( accuracy_xgbm_sm))
roc_auc_sm = roc_auc_score(test_y, xgb_model_sm_pred)
print('roc score : {:0.3f}'.format( roc_auc_sm))
dump(xgb_model_sm, '/content/drive/My Drive/ImbalancedData/xgb_model_sm.joblib')
xgb_model_sm = load('/content/drive/My Drive/ImbalancedData/xgb_model_sm.joblib')
xgb_model_sm_pred = xgb_model_sm.predict_proba(test_x.values)[:,1]
Evaluate(labels=test_y, predictions=xgb_model_sm_pred, p=0.5)
Legitimate Transactions Detected (True Negatives): 56306
Fraudulent Transactions Missed (False Negatives): 6
Fraudulent Transactions Detected (True Positives): 99
Legitimate Transactions Incorrectly Detected (False Positives):551
Total Fraudulent Transactions: 105
auc :0.9948591160614306
precision :0.1523076923076923
recall :0.9428571428571428
f1 :0.2622516556291391
Area Under PR Curve(AP): 0.5458
Forest of randomized trees
BalancedRandomForestClassifier is another ensemble method in which each tree of the forest will be provided a balanced bootstrap sample. This class provides all functionality of the sklearn.ensemble.RandomForestClassifier and notably the feature_importances_ attributes:
from imblearn.ensemble import BalancedRandomForestClassifier
brf = BalancedRandomForestClassifier(n_estimators=100, random_state=0)
brf.fit(train_x, train_y )
brf_pred = brf.predict(test_x)
balanced_accuracy_score(test_y, brf_pred)
#brf.feature_importances
dump(brf, '/content/drive/My Drive/ImbalancedData/brf.joblib')
brf = load('/content/drive/My Drive/ImbalancedData/brf.joblib')
brf_pred = brf.predict_proba(test_x.values)[:,1]
Evaluate(labels=test_y, predictions= brf_pred, p=0.5)
Legitimate Transactions Detected (True Negatives): 55509
Fraudulent Transactions Missed (False Negatives): 2
Fraudulent Transactions Detected (True Positives): 103
Legitimate Transactions Incorrectly Detected (False Positives):1348
Total Fraudulent Transactions: 105
auc :0.9878704887868227
precision :0.0709855272226051
recall :0.9809523809523809
f1 :0.13239074550128535
Area Under PR Curve(AP): 0.5241
RusBoost
from imblearn.ensemble import RUSBoostClassifier
from sklearn.datasets import make_classification
rbt = RUSBoostClassifier(random_state=0,
base_estimator=DecisionTreeClassifier(),
sampling_strategy='auto')
# Fit the grid search to the data
rbt.fit(X=train_x, y=train_y)
dump(rbt, '/content/drive/My Drive/ImbalancedData/rbt.joblib')
rbt = load('/content/drive/My Drive/ImbalancedData/rbt.joblib')
rbt_pred = rbt.predict_proba(test_x.values)[:,1]
Evaluate(labels=test_y, predictions= rbt_pred, p=0.5)
Legitimate Transactions Detected (True Negatives): 55970
Fraudulent Transactions Missed (False Negatives): 5
Fraudulent Transactions Detected (True Positives): 100
Legitimate Transactions Incorrectly Detected (False Positives):887
Total Fraudulent Transactions: 105
auc :0.9918764452507
precision :0.10131712259371833
recall :0.9523809523809523
f1 :0.18315018315018314
Area Under PR Curve(AP): 0.5250
EasyEnsembleClassifier
A specific method which uses AdaBoost as learners in the bagging classifier is called EasyEnsemble. The EasyEnsembleClassifier allows to bag AdaBoost learners which are trained on balanced bootstrap sample. Similarly to the BalancedBaggingClassifier API, one can construct the ensemble as:
from imblearn.ensemble import EasyEnsembleClassifier
eec = EasyEnsembleClassifier(random_state=0,
base_estimator=AdaBoostClassifier(),
sampling_strategy='auto')
eec.fit(X=train_x, y=train_y)
dump(eec, '/content/drive/My Drive/ImbalancedData/eec.joblib')
eec = load('/content/drive/My Drive/ImbalancedData/eec.joblib')
eec_pred = eec.predict_proba(test_x.values)[:,1]
Evaluate(labels=test_y, predictions= eec_pred, p=0.5)
Legitimate Transactions Detected (True Negatives): 54565
Fraudulent Transactions Missed (False Negatives): 3
Fraudulent Transactions Detected (True Positives): 102
Legitimate Transactions Incorrectly Detected (False Positives):2292
Total Fraudulent Transactions: 105
auc :0.9912644671636528
precision :0.042606516290726815
recall :0.9714285714285714
f1 :0.08163265306122448
Area Under PR Curve(AP): 0.5052
Bagging classifier
BalancedBaggingClassifier allows to resample each subset of data before to train each estimator of the ensemble. In short, it combines the output of an EasyEnsemble sampler with an ensemble of classifiers (i.e. BaggingClassifier). Therefore, BalancedBaggingClassifier takes the same parameters than the scikit-learn BaggingClassifier. Additionally, there is two additional parameters, sampling_strategy and replacement to control the behaviour of the random under-sampler:
from imblearn.ensemble import BalancedBaggingClassifier
from imblearn.ensemble import BalancedBaggingClassifier
bbc = BalancedBaggingClassifier(base_estimator=DecisionTreeClassifier(),
sampling_strategy='auto',
replacement=False,
n_jobs=-1,
random_state=0)
bbc.fit(X=train_x, y=train_y)
dump(bbc, '/content/drive/My Drive/ImbalancedData/bbc.joblib')
bbc_model = load('/content/drive/My Drive/ImbalancedData/bbc.joblib')
bbc_pred = bbc_model.predict_proba(test_x.values)[:,1]
Evaluate(labels=test_y, predictions= bbc_pred, p=0.5)
Legitimate Transactions Detected (True Negatives): 55701
Fraudulent Transactions Missed (False Negatives): 5
Fraudulent Transactions Detected (True Positives): 100
Legitimate Transactions Incorrectly Detected (False Positives):1156
Total Fraudulent Transactions: 105
auc :0.9845647853386567
precision :0.07961783439490445
recall :0.9523809523809523
f1 :0.1469507714915503
Area Under PR Curve(AP): 0.5142
#pred_df=pd.DataFrame()
pred_df = pd.DataFrame(test_y,index=None)
pred_df['baggingclassifier_pred'] =bbc_pred
pred_df['easyensemble_pred'] = eec_pred
pred_df['RusBoost_pred'] = rbt_pred
pred_df['forest_r_t'] = brf_pred
pred_df['xgb_rus_pred'] = xgb_model_rus_pred
pred_df['xgb_smote_pred'] = xgb_model_sm_pred
pred_df['xgboost_weights'] = ns_model_pred
#pred_df["test_y"] = test_y
pred_df["xgb_no_weights_pred"] = xgb_no_weights_pred
pred_df.to_csv('/content/drive/My Drive/ImbalancedData/pred_df.csv')
#
#pred_df.head()
#pred_df.test_y.isna().sum()
#test_y
#test_y.isna().sum()
Plot the AUC ROC
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
from sklearn.metrics import roc_curve
def plot_roc(name, labels, predictions, p=0.5, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,80])
plt.title('Area Under ROC Curve @{:.2f}'.format(p))
plt.ylim([20,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
#%matplotlib inline
sns.set_style("whitegrid")
plot_roc("xgboost No Weight", test_y, xgb_no_weights_pred, color=colors[0],linestyle='--')
plot_roc("Xgboost Weight", test_y ,ns_model_pred, color=colors[1])
plot_roc("Xgboost Under-Sampling", test_y, xgb_model_rus_pred, color=colors[2])
plot_roc("Xgboost Smote", test_y ,xgb_model_sm_pred, color=colors[3])
plot_roc("Forest of Randomized Trees", test_y ,brf_pred, color=colors[4])
plot_roc("RusBoost", test_y ,rbt_pred, color=colors[5])
plot_roc("EasyEnsemble Classifier", test_y ,eec_pred, color=colors[6])
plot_roc("Bagging Classifier", test_y ,bbc_pred, color=colors[7])
plt.legend(loc='lower right')
plt.savefig('/content/drive/My Drive/ImbalancedData/all_rocauc.png')
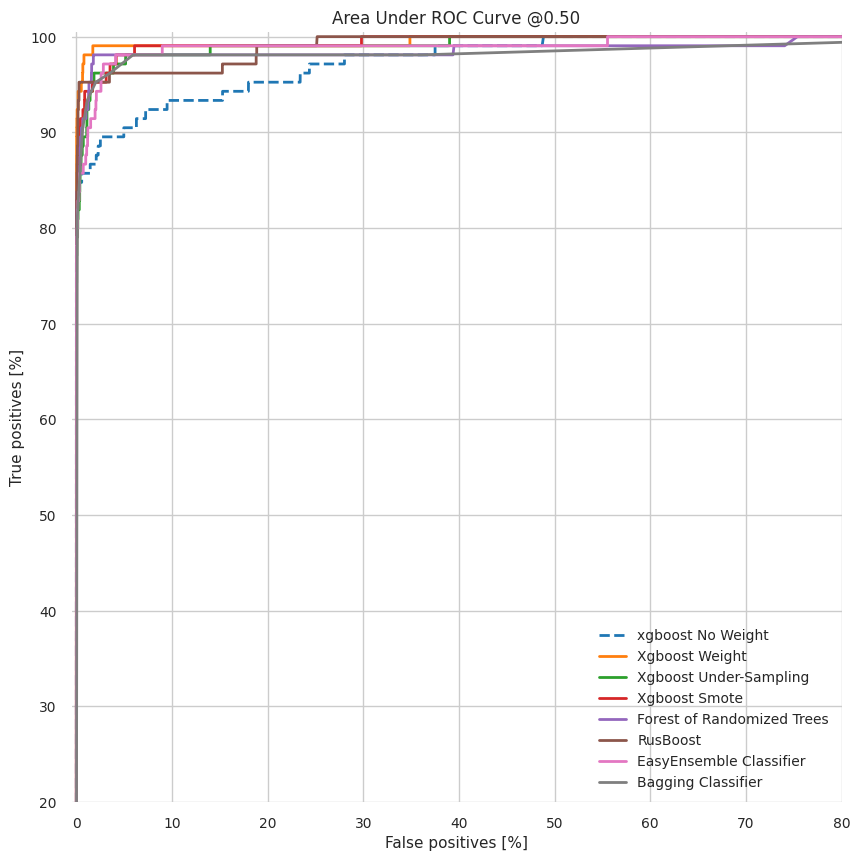
Plot the Area Under Orecision Recall Curve
from sklearn.metrics import precision_recall_curve
def plot_auc_pr(name, labels, predictions,n=0.5, **kwargs):
p, r, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(100*r, 100*p, label=name, linewidth=2, **kwargs)
plt.xlabel('Recall [%]')
plt.ylabel('Precision [%]')
plt.xlim([-0.5,100])
plt.title('Area Under Precision-Recall Curve @{:.2f}'.format(n))
#plt.title('Area Under Precision-Recall Curve: {}' .format(p))
plt.ylim([20,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
#plot_auc_pr("Train Weight", train_labels, train_predictions_weight, color=colors[1])
sns.set_style("whitegrid")
plot_auc_pr("xgboost No Weight", test_y, xgb_no_weights_pred, color=colors[0],linestyle='--')
plot_auc_pr("Xgboost Weight", test_y ,ns_model_pred, color=colors[1])
plot_auc_pr("Xgboost Under-Sampling", test_y, xgb_model_rus_pred, color=colors[2])
plot_auc_pr("Xgboost Smote", test_y ,xgb_model_sm_pred, color=colors[3])
plot_auc_pr("Forest of Randomized Trees", test_y ,brf_pred, color=colors[4])
plot_auc_pr("RusBoost", test_y ,rbt_pred, color=colors[5])
plot_auc_pr("EasyEnsemble Classifier", test_y ,eec_pred, color=colors[6])
plot_auc_pr("Bagging Classifier", test_y ,bbc_pred, color=colors[7])
plt.legend(loc='lower left')
plt.savefig('/content/drive/My Drive/ImbalancedData/auc_pr2.png')
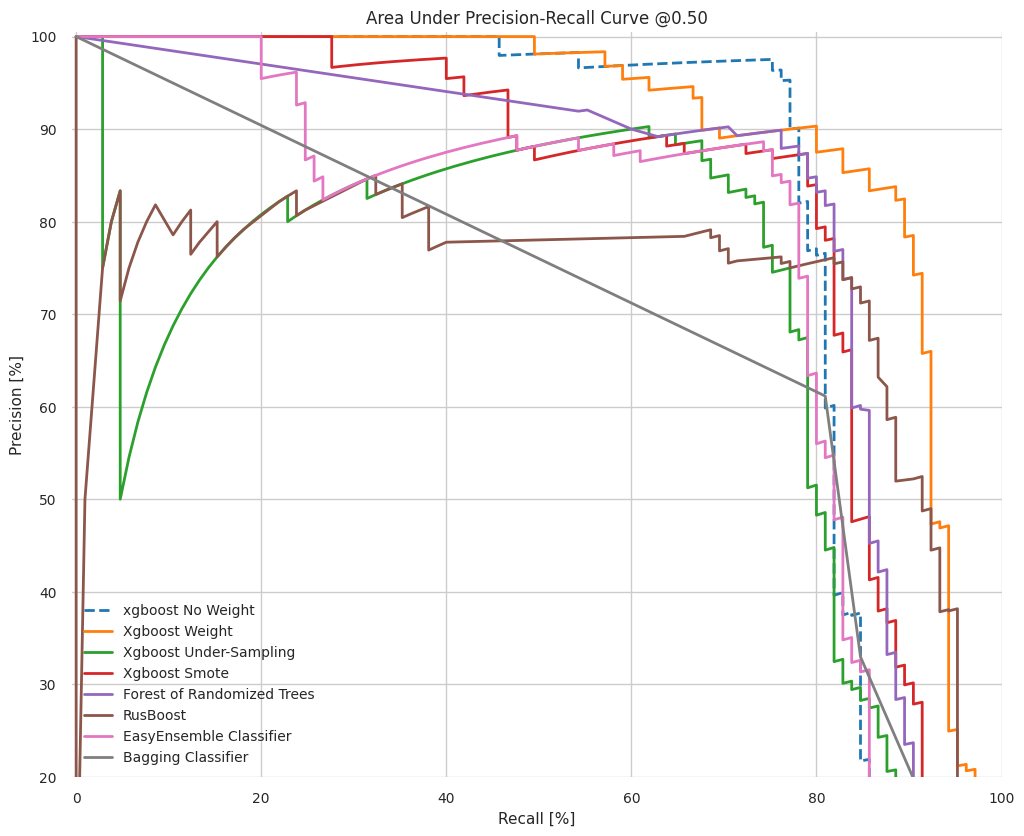
Cost-Sensitive Logistic Regression
Logistic Regression is a well known statistical model for modeling binary target values that is often overlooked. It will be interesting to see how it performs when presented with an imbalanced target class. It can be modified to perform a Cost-sensitive learning with imbaalanced data.
from sklearn.linear_model import ElasticNet
from sklearn import linear_model
elasticreg = linear_model.SGDClassifier( tol=1e-3,
class_weight='balanced',
max_iter = int(1e4),
warm_start = True,
n_jobs = -1)
plt.style.use('ggplot')
sns.set_style("whitegrid")
threshhold=0.5
fig = plt.figure(figsize=(15,8))
ax1 = fig.add_subplot(1,2,1)
ax1.set_xlim([0,100])
ax1.set_ylim([0,100])
ax1.set_xlabel('Recall')
ax1.set_ylabel('Precision')
ax1.set_title('Area Under Precision-Recall Curve @{:.2f}'.format(threshhold))
ax2 = fig.add_subplot(1,2,2)
ax2.set_xlim([-0.5,30])
ax2.set_ylim([80,100])
ax2.set_xlabel('False Positive Rate')
ax2.set_ylabel('True Positive Rate')
ax2.set_title('Area Under ROC Curve @{:.2f}'.format(threshhold))
rocauc_vector= []
f1_vector= []
prec_vector= []
rec_vector= []
#cfn_matrix_ = np.zeros((8, 4))
cfn_matrix_ =[]
pr_auc_vector =[]
for w,k in zip([1,5,10,20,50,100,500,10000],'bgrcmykw'):
lr_model = LogisticRegression(class_weight={0:1,1:w})
lr_model.fit(train_x,train_y)
threshhold=0.5
pred_prob = lr_model.predict_proba(test_x)[:,1]
p,r,_ = precision_recall_curve(test_y,pred_prob)
tpr,fpr,_ = roc_curve(test_y,pred_prob)
auc= roc_auc_score(test_y,pred_prob)
f1 = f1_score(test_y,pred_prob >threshhold )
#f1 = f1_score(labels, predictions> threshhold)
prec=precision_score(test_y,pred_prob>threshhold)
rec=recall_score(test_y,pred_prob > threshhold)
cfn_matrix = confusion_matrix(test_y,pred_prob > threshhold)
rocauc_vector.append(auc)
f1_vector.append(f1)
prec_vector.append(prec)
rec_vector.append(rec)
#cfn_matrix_[w,:] = cfn_matrix.flatten()
cfn_matrix_.append(cfn_matrix)
precision, recall, thresholds = precision_recall_curve(test_y, pred_prob > threshhold)
#use the trapezoidal rule to calculate the area under the precion-recall curve
area = trapz(recall, precision)
pr_auc_vector.append(area)
ax1.plot(r*100,p*100,c=k,label=w)
ax2.plot(tpr*100,fpr*100,c=k,label=w)
#plt.xlim([-0.5,30])
#plt.title('Area Under ROC Curve @{:.2f}'.format(p))
#plt.ylim([80,100.5])
ax1.legend(loc='lower left')
ax2.legend(loc='lower right')
plt.savefig('/content/drive/My Drive/ImbalancedData/logistic.png')
plt.show()
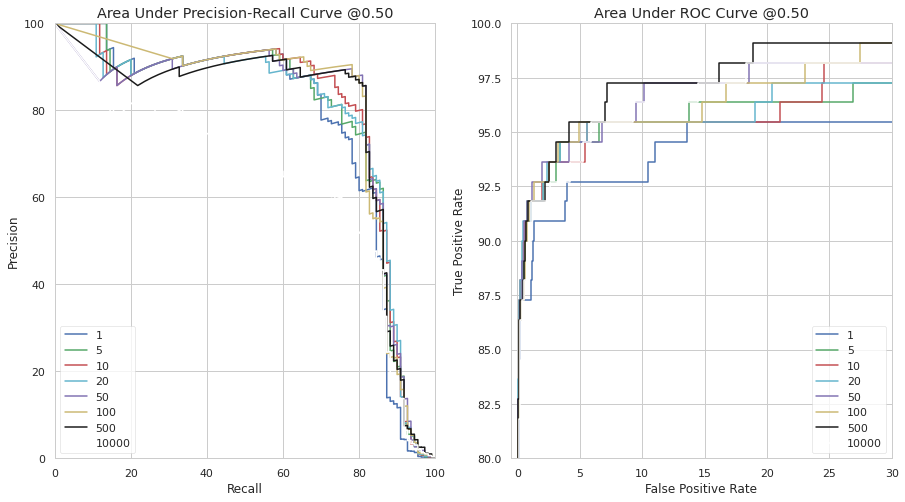
results=pd.DataFrame(list(zip([1,5,10,20,50,100,500,10000],rocauc_vector,f1_vector,prec_vector,rec_vector)))
results.columns = ['Weight','ROC_AUC','F-Score','Precision','Recall']
results['TP'] = [66,83,89,92,95,96,101,108]
results['TN'] = [56846,56831,56829,56805,56750,56613,55668,40576]
results['FP'] = [6,21,23,47,102,239,1184,16276]
results['FN'] = [46,27,21,18,15,14,9,2]
results['PR_AUC'] = pr_auc_vector
results
|
Weight |
ROC_AUC |
F-Score |
Precision |
Recall |
TP |
TN |
FP |
FN |
PR_AUC |
| 0 |
1 |
0.959148 |
0.725275 |
0.916667 |
0.600000 |
66 |
56846 |
6 |
46 |
0.756788 |
| 1 |
5 |
0.976090 |
0.775701 |
0.798077 |
0.754545 |
83 |
56831 |
21 |
27 |
0.774617 |
| 2 |
10 |
0.978801 |
0.801802 |
0.794643 |
0.809091 |
89 |
56829 |
23 |
21 |
0.800120 |
| 3 |
20 |
0.982562 |
0.738956 |
0.661871 |
0.836364 |
92 |
56805 |
47 |
18 |
0.747344 |
| 4 |
50 |
0.985512 |
0.618893 |
0.482234 |
0.863636 |
95 |
56750 |
102 |
15 |
0.671135 |
| 5 |
100 |
0.986236 |
0.431461 |
0.286567 |
0.872727 |
96 |
56613 |
239 |
14 |
0.577839 |
| 6 |
500 |
0.988871 |
0.144803 |
0.078599 |
0.918182 |
101 |
55668 |
1184 |
9 |
0.496538 |
| 7 |
10000 |
0.986018 |
0.013096 |
0.006592 |
0.981818 |
108 |
40576 |
16276 |
2 |
0.492291 |
Cost-sensitive logistic regression with a weight of 10 on the minority class performs well in comparison to other weights. It has a high ROC-AUC and area under the precision-recall curve.


